| Angelika Langer - Training & Consulting |
| HOME | |

|
|

|
|

OVERVIEW
BY COLUMN
BY MAGAZINE
|
|
| GENERICS | |
| LAMBDAS | |
| IOSTREAMS | |
| ABOUT | |
| CONTACT |
|
C++ Expression Templates
An Introduction to the Principles of Expression Templates
Draft version of an article published
in C/C++ Users Journal, March 2003
|
[There is a Russian translation available at CPP-REFERENCE.RU and a Chinese one at BLOG.CSDN.NET .] |
Templates were introduced to the C++ programming language as a means
to express parameterized types. The prototypical example of a parameterized
type is a list, of which you do not want to implement a separate version
for each type of element maintained in that list. Instead you want
to provide one list implementation (the template), which uses a placeholder
for the element type (the template parameter), from which the compiler
can generate different list classes (the instantiations of the template).
Today templates are used in ways that the inventors of C++ templates certainly hadn't anticipated. Template programming these day includes techniques such as generic programming, compile-time computations, expression template libraries, template meta-programming, and generative programming, just to name a few. In this article we aim to explain some of the principles of expression templates and more specifically the programming techniques that are used to build expression template libraries.
To say it right away: expression template libraries are complex.
For this reason, pretty much every explanation of expression templates
that we've read so far got rather challenging and advanced pretty rapidly.
The ambitious goal of this article is making complex matters easy so that
they can be understood without getting lost in all the details that you
would find otherwise, if for instance you studied the source code of a
template library. We will try to distill some of the principles of
expression templates; yet full coverage of all aspects of expressions templates
is beyond the scope of the article.
Table of Contents
- An Introduction to the Principles of Expression Templates
- Where it all started ...
- A First Example of a Compile-Time Computation - Factorial
- Another Example of a Compile-Time Computation - Square Root
- Moving on to Expression Templates
- A First Expression Template - Dot Product
- A Compile-Time Version of the Dot Product
- Another Expression Template - Arithmetic Expressions
- Creator Functions
- Further Elaboration of the Expression Template Solution
- Traits
- Repeated Evaluation of an Expression Object
- References
Where it all started ...
I vividly remember the day when a colleague of mine, Erwin Unruh, stepped into one of these C++ standards committee meetings proudly presenting a program that did not compile, yet it calculated the prime numbers (see / UNR /). It emitted error messages when it was compiled and with each of the error messages the next prime number was printed. Of course, it is nonsensical to write programs that do not compile, but this program was deliberately set up so that it would not compile in order to point out that this was a computation that was done at compile-time. There was no executable, nothing happening at run time. The prime number computation was a side effect of the compilation.
This tiny silly program treaded off an avalanche of research and experimentation
in the following years which lead to what is known as template meta-programming
these days. In this article we will discuss some of the resulting programming
techniques and principles.
How does Template Meta-Programming Work?
Basically, the prime number calculation and many of the techniques that
we will explain in this article build on the fact that instantiation of
templates is a recursive process. When the compiler instantiates
a template it might find that for the instantiation of one template it
might need an instantiation of another template. It then instantiates
that other template, which might require the instantiation of yet another
template, and so on and so forth. Many of the template meta-programming
techniques take advantage of the recursive nature of the template instantiation
process and use it to perform recursive calculations.
A First Example of a Compile-Time Computation - Factorial
As a first example let us calculate the factorial of N at compile time. The factorial of n (the mathematical notation of which is n!) is the product of all number from 1 to n., the factorial of 0 being 1. Normally, without use of templates, you would calculate the factorial by means of recursive function calls. Here is a conceivable runtime implementation:
int factorial (int n)
{ return (n==0) ? 1: n*factorial(n-1); }
This function calls itself recursively until n drops down to 0. It would be used like this:
cout << factorial(4) << endl;
Recursive function calls are expensive, especially since the compiler will probably refuse to inline the recursive calls and we will end up with quite a number of function calls. We can do better than that - using compile-time computations instead. It goes like this: replace the recursive function calls by recursive template instantiations. Instead of providing a function named factorial we will implement a class named factorial. To be more precise it will be a class template named factorial. Here it is:
template <int n>
struct factorial {
enum { ret = factorial<n-1>::ret * n };
};
This class template has neither data nor function members, it just defines an unnamed enum type with exactly one enum value. (As it will turn out later, this enum value factorial::ret will serve as the return value of our compile time calculation.) In order to compute the value of this enum the compiler must instantiate another version of the factorial template, namely the version for n-1, and this is what starts the recursive template instantiation.
Note, that the template argument of the factorial template is kind of unusual: it is a non-type template argument, namely a constant value of type int. Usually, templates have type arguments like in template <class T> class X { ...}; where T is a placeholder for a concrete type that will later replace the placeholder T when a class like X<int> will be generated from the class template. In our example we have a non-type template argument of type int, which means that this template will be instantiated providing a constant value of type int. Using this factorial class template a user would calculate the factorial of n as follows:
cout << factorial<4>::ret << endl;
The compiler would recursively instantiate factorial<4>, and factorial<3>, and so on and so forth, until ... actually, until when? How does this recursion come to a halt? Every recursion needs an end. Using the template technique the end of the recursion is provided by means of a template specialization. In our example the specialization is for the case that n equals 0:
template <>
struct factorial<0> {
enum { ret = 1 };
};
As you can tell from the code snippet above the recursion will stop here because the value of the enum value ret does not depend on any further instantiations of the factorial template anymore.
If you are not familiar with template specialization, don't worry. Just make a mental note that a special version of a class template can be provided for special template arguments. In our example we provide a special implementation of the factorial template for the case that the template argument n is 0. And this specialization will end the recursion.
Now, what have we achieved using the template version of the computation
of a factorial? Well, the expression factorial<4>::ret will boil
down to a mere 24 (which is the value of 4!) at run time, that is, in the
executable you will not find any computation at all. Instead there
will simply be the constant value 24 in the executable in all places where
factorial<4>::ret appears in the source code.
Another Example of a Compile-Time Computation - Square Root
Let's try it again and study another compile-time computation of a value. This time we aim to approximate the square root of N, or more precisely we want to find the integral value greater and closest to the square root of N. Example: the square root of 10 is 3.1622776601; that is, we would like to find the integral value 4, which is the next integer greater than 3.1622776601. Using runtime calculations we can calculate the desired value using C library functions as ceil(sqrt(N)). However, we want to use the approximated square root as the size of an array that we need to declare, but a declaration such asint array[ceil(sqrt(N))];
is illegal because the array size must be a compile-time constant value. For this reason we need to approximate the square root at compile-time.
Remember , what we did in our first example of a compile-time computation:
we took advantage of recursive template instantiation. Again, we
will trigger a recursive template instantiation to approximate the desired
value. Again, we will define a class template that takes a non-type template
argument, namely N, and returns the result in form of a nested value.
Let's call the class template for our square root approximation Root. We
could then declare an array of the size of square root of 10 as
int array[Root<10>::ret];
Here is the class template Root:
template <size_t N, size_t Low=1, size_t Upp=N>
struct Root {
static const size_t ret = Root<N,(down?Low:mean+1),(down?mean:Upp)>::ret;
static const size_t mean = (Low+Upp)/2;
static const bool down = ((mean*mean)>=N);
};
We don't want to delve into the details here. Just a couple of comments: The class template takes 3 non-type template arguments, 2 of which have defaults. The 3 arguments are
- the value whose square root is to be calculated and
- the lower and upper bound of an interval in which the result will be located. The default values are 1 and N because the square root of N will be a value somewhere between 1 and N.
Where does the recursion end? Again, the end of the recursion is specified by means of a template specialization that does not require any further template instantiations. Here is the specialization of the Root class template:
template <size_t N, size_t Mid>
struct Root<N,Mid,Mid>
{ static const size_t ret = Mid; };
Note that the specialization has only 2 template arguments. This is because the recursion ends when the interval in which the result lies collapses to a single value, namely the desired result.
In our example the recursion will instantiate the template for the following
arguments:
Root<10,1,10>
Root<10,1,5>
Root<10,4,5>
Root<10,4,4>
and the result will be 4, as expected.
The point to take home from these two examples is that compile-time
computations are often recursive processes that take advantage of the recursive
nature of the template instantiation process. What would be a function
in a runtime computation is typically a class template in a compile-time
computation. What would be the argument of a function in a runtime
computation is typically a non-type template argument in a compile-time
computation. What would be the return value of a function in a runtime
computation is typically the a nested constant in the class template in
a compile-time computation. And the condition that ends the recursion in
a runtime computation is typically a template specialization in a compile-time
computation. Equipped with this knowledge, it is no long stretch
anymore to imagine how Erwin Unruh's prime number calculation was built
on the exact same principles that we've been using in our two calculations.
Moving on to Expression Templates
So far we have been calculating values at compile-time, which is nice, but not overly exciting. Let's get more ambitious: let's evaluate more complex expressions at compile-time. In a first step, we will implement a compile-time version of a vector dot product. The dot product of two vectors is the sum of the products of its corresponding elements. Example: The dot product of the two 3-dimensional vectors (1,2,3) and (4,5,6) would be 1*4 + 2*5 + 3*6, which is 32. The goal is to set up expression templates for the calculation of the dot product of vectors of arbitrary dimensions, like in the following example:
int a[4] = {1,100,0,-1};
int b[4] = {2,2,2,2};
cout << dot<4>(a,b);
The dot product is a first primitive example of an expression template, but the techniques that we will apply for the vector dot product have been generalized for arithmetic operations on multi-dimensional matrices. Naturally, the gain in runtime performance that the compile-time computation will provide, is much more dramatic for a matrix operation than it is for a vector dot product. The techniques however are based on the same principles.
Another powerful generalization is the use of expression templates in
a more dynamic fashion: we eventually want to evaluate an expression repeatedly,
passing in different values for each expression evaluation. By means
of expression templates these evaluations would be performed at compile-time
incurring zero overhead at runtime. Expression evaluations play a
role in the calculation of integrals, for instance. An example:
the integral
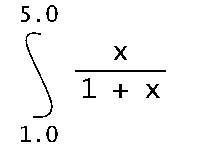
can be approximated by evaluating the expression x/(1+x) for n equidistant
points in the interval [1.0,5.0]. A function that calculates integrals
for arbitrary arithmetic expressions could look like this, provided we
manage to implement expression templates that can be evaluated repeatedly
for different values:
template <class ExprT>
double integrate (ExprT e,double from,double to,size_t n)
{ double sum=0, step=(to-from)/n;
for (double i=from+step/2; i<to; i+=step)
sum+=e.eval(i);
return step*sum;
}
ExprT in this example would somehow represent an expression such as
x/(1+x). We will see how exactly it works later in the article.
A First Expression Template - Dot Product
In order to distill the essence of expression templates let us explain the vector dot product and the arithmetic expressions, which we will explore later, in terms of commonly known patterns as described in the classic patterns book by Gamma et.al. (/ GOF /). A vector dot product can be seen as a special case of a composite.The Composite pattern provides a way to represent a part-whole relationship where the client can ignore the difference between individual objects and compositions of objects. The key elements of the Composite pattern are the leaf and the composite:
- The leaf defines the behavior for primitive objects in the composition.
- The composite defines the behavior for components consisting of leaves.
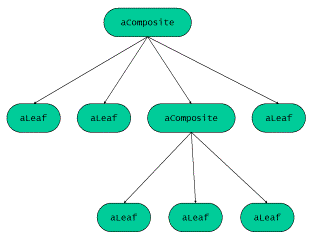
Figure 1: A Typical Composite Structure
The GOF book suggests an object-oriented implementation of the Composite
pattern with an abstract base class, which defines the operation that leaves
and composites have in common and two derived classes, which represent
the leaf and the composite respectively.
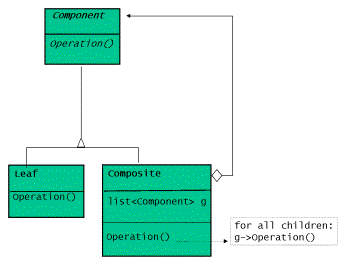
Figure 2: Class diagram of the Composite pattern
The vector dot product can be seen as a special case of the Composite
pattern. A dot product can be split into a leaf (namely the dot product
of two vectors of dimension 1) and a composite (namely the dot product
of the two vectors of dimension N-1).
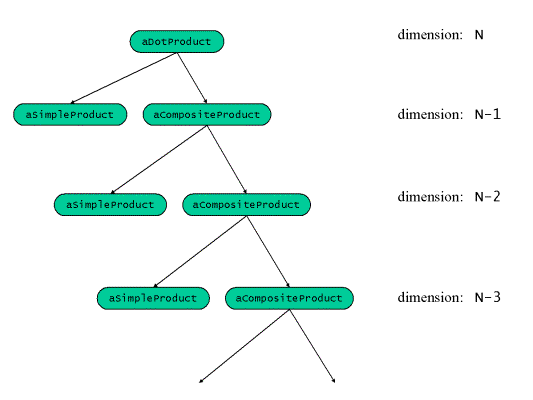
Figure 3: Composite Structure of a Dot Product
Obviously, this is a degenerated form of the prototypical composite
because each composite consists of exactly one leaf and one composite.
Using the suggested object-oriented implementation technique we would represent
the dot product by a base class and two derived classes as shown in the
class diagram below:
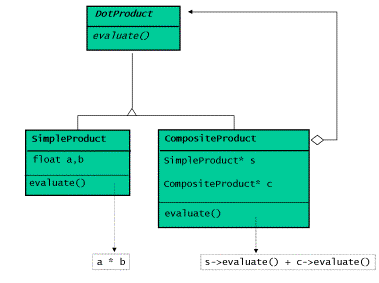
F
igure 4: Class Diagram of Dot Product as a Composite
The implementation is straightforward and shown in Listing 1 thru 3.
Listing 4 shows a helper function that eases use of these classes and Listing
5 eventually demonstrates how we can calculate the dot product of
two vectors.
| Listing 1: The Base Class |
|
template <class T> class DotProduct { public: virtual ~DotProduct () {} virtual T eval() = 0; }; |
| Listing 2: The Composite |
|
template <class T> class CompositeDotProduct : public DotProduct<T> { public: CompositeDotProduct (T* a, T* b, size_t dim) :s(new SimpleDotProduct<T>(a,b)) ,c((dim==1)?0:new CompositeDotProduct<T>(a+1,b+1,dim-1)) {} virtual ~CompositeDotProduct () { delete c; delete s; } virtual T eval() { return (s->eval() + ((c)?c->eval():0)); } protected: SimpleDotProduct<T>* s; CompositeDotProduct<T> * c; }; |
| Listing 3: The Leaf |
|
template <class T> class SimpleDotProduct : public DotProduct<T> { public: SimpleDotProduct (T* a, T* b) :v1(a), v2(b) {} virtual T eval() { return (*v1)*(*v2); } private: T* v1; T* v2; }; |
| Listing 4: Helper Function |
|
template <class T> T dot(T* a, T* b, size_t dim) { return (dim==1) ? SimpleDotProduct<T>(a,b).eval() : CompositeDotProduct<T>(a,b,dim).eval(); } |
| Listing 5: Using the Dot Product Implementation |
|
int a[4] = {1,100,0,-1}; int b[4] = {2,2,2,2}; cout << dot(a,b,4); |
Naturally, this is not the most efficient way of calculating the dot product of two vectors. We can substantially simplify the implementation by eliminating the representation of the composite and the leaf object as data members in the derived classes. Instead of passing the vectors to the leaf and the composite at construction time and memorizing them for subsequent evaluation we could pass the information directly to the evaluation function.
Constructor and evaluation function
SimpleDotProduct<T>::SimpleDotProduct (T* a, T* b) :v1(a), v2(b)
{}
virtual T SimpleDotProduct<T>::eval() { return (*v1)*(*v2);
}
would be replaced by an evaluation function that takes arguments:
T SimpleDotProduct::eval(T* a, T* b, size_t dim) { return (*a)*(*b); }
The simplified implementation of the derived classes is shown in Listing
6; the base class would remain unchanged as shown in Listing 1; the helper
function must be adjusted.
| Listing 6: A Simplified Object-Oriented Implementation of the Vector Dot Product |
|
template <class T> class CompositeDotProduct : public DotProduct <T> { public: virtual T eval(T* a, T* b, size_t dim) { return SimpleDotProduct<T>().eval(a,b,dim) + ((dim==1) ? 0 : CompositeDotProduct<T>().eval(a+1,b+1,dim-1)); } };
template <class T>
|
Figure 5 shows the corresponding class diagram for the simplified solution.
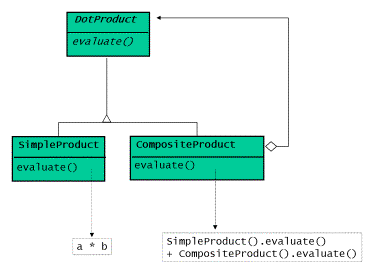
Figure 5: Class Diagram of a Simplified Dot Product Implementatio
n
A Compile-Time Version of the Dot Product
Let us now take the object-oriented approach and translate it to a compile-time solution. The two classes representing the leaf and the composite have a common base class that defines the operation that they have in common. This is a well-known technique in object-orientation: commonalities are expressed by means of a common base class. In template programming, commonalities are expressed in terms of naming conventions and name commonalities. What is a virtual function in the object-oriented approach will become a plain non-virtual function that has a certain name. The two derived classes will no longer be derived from a common base class. Instead they will be stand-alone classes that happen to have a member function with the same name and a compatible signature. That is, we will eliminate the base class.Next, we will implement the composite as a class template using structural information as template arguments. This structural information is the dimension of the vectors. Remember what we did for the calculation of the factorial and the square root: the former function argument in the runtime implementation became a template argument in the compile-time implementation. We will be doing a similar thing here: the vectors' dimension is passed as an argument to the evaluation function in the object-oriented approach; we will pass it as a template argument in the compile-time implementation. Hence the dimension of the vectors will be become a non-type template argument of the composite class.
The leaf will be implemented as a specialization of the composite class template for dimension N = 1. As before we will replace the runtime recursion by a compile-time recursion: we will replace the recursive invocation of the virtual evaluation function by recursive template instantiation of a static evaluation function. Here is the class diagram of our compile-time implementation of the vector dot product:
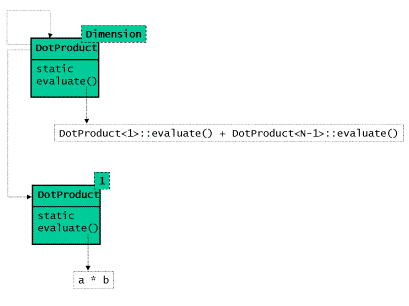
Figure 6: Class Diagram of a Compile-Time Implementation of the
Dot Product
The implementation is shown in Listing 7. Usage of the implementation
is shown in Listing 8.
| Listing 7: The Compile-Time Implementation of the Dot Product |
|
template <size_t N, class T> class DotProduct { public: static T eval(T* a, T* b) { return DotProduct<1,T>::eval(a,b) + DotProduct<N-1,T>::eval(a+1,b+1); } };
template <class T>
|
| Listing 8: Using the Dot Product Implementation |
|
template <size_t N, class T> inline T dot(T* a, T* b) { return DotProduct<N,T>::eval(a,b); }
int a[4] = {1,100,0,-1};
|
Note the difference between the expressions dot(a,b,4) in the runtime implementation and dot<4>(a,b) in the compile-time implementation:
dot(a,b,4)
evaluates to
CompositeDotProduct<size_t>().eval(a,b,4)
which recursively triggers the following function calls as runtime:
SimpleDotProduct<size_t>().eval(a,b,1), CompositeDotProduct<size_t>().eval(a+1,b+1,3),
SimpleDotProduct<size_t>().eval(a+1,b+1,1), CompositeDotProduct<size_t>().eval(a+2,b+2,2),
SimpleDotProduct<size_t>().eval(a+2,b+2,1), CompositeDotProduct<size_t>().eval(a+3,b+3,1),
SimpleDotProduct<size_t>().eval(a+3,b+3,1),
which sums up to a total of 7 virtual function calls.
dot<4>(a,b)
on the other hand evaluates to
DotProduct<4,size_t>::eval(a,b)
which
recursively triggers instantiation of further class templates and gradually
unfolds as follows:
DotProduct<4,size_t>::eval(a,b)
evaluates to
DotProduct<1,size_t>::eval(a,b) + DotProduct<3,size_t>::eval(a+1,b+1)
which evaluates to
(*a)*(*b) + DotProduct<1,size_t>::eval(a+1,b+1) + DotProduct<2,size_t>::eval(a+2,b+2)
which evaluates to
(*a)*(*b) + (*a+1)*(*b+1) + DotProduct<1,size_t>::eval(a+2,b+2)
+ DotProduct<1,size_t>::eval(a+3,b+3)
which evaluates to
(*a)*(*b) + (*a+1)*(*b+1) + (*a+2)*(*b+2) + (*a+3)*(*b+3)
.
Visible in the executable is only the resulting expression
(*a)*(*b)
+ (*a+1)*(*b+1) + (*a+2)*(*b+2) + (*a+3)*(*b+3)
; the recursive template
instantiation itself will have been performed at compile-time already.
Evidently the template approach to the problem is significantly more efficient in terms of runtime performance - at the expense of increased compilation time. The recursive template instantiation takes time and not surprisingly the compile time consumption goes up by orders of magnitude for the template solution compared to the object-oriented solution, which compiles fast, but runs slowly.
Another limitation of the template solution is that the dimension of the vectors must be known at compile-time because the dimension is a template argument of the DotProduct template. In practice this is not much of a restriction because the vector dimension is often known in advance; in many applications we simply know that we will be performing arithmetic operation on 3-dimensional vectors representing points in space, for instance.
The implementation of the vector dot product might no be overly impressive,
after all we could have achieved the same high performance by unfolding
the dot product expression manually. But the techniques demonstrated here
for implementation of the dot product can be generalized to arithmetic
operations on multi-dimensional matrices. The real benefit of the
solution lies in its expressiveness. Imagine an expression such as
a*b+c, where a, b and c are 10x20 matrices. You would not want to
unfold the resulting expression manually, if the compiler can do it automatically
and reliably.
Another Expression Template - Arithmetic Expressions
Let us know take the techniques one step further and consider a real composite structure: arithmetic expressions consisting of unary and binary arithmetic operators and variable and constant operands. The GOF book has a pattern for exactly this case - the Interpreter pattern.The Interpreter pattern provides a way to represent a language in form of an abstract syntax tree and an interpreter that uses the syntax tree to interpret language constructs. It is a special case of the Composite pattern. The part-whole relationship of the Composite pattern corresponds to the relationship of an expression and its subexpressions in the Interpreter pattern.
- The leaf is a terminal expression.
- The composite is a non-terminal expression.
- Evaluation of the components is interpretation of the syntax tree and its expressions.
Let us take the concrete example of an expression, say (x+2)*3. The
composite structure, that is, the syntax tree for this expression would
look like this:

Figure 7: Example of a Syntax Tree for an Arithmetic Expression
The classic object-oriented technique for implementing the Interpreter pattern, as it is suggested in the GOG book, would involve the following classes:
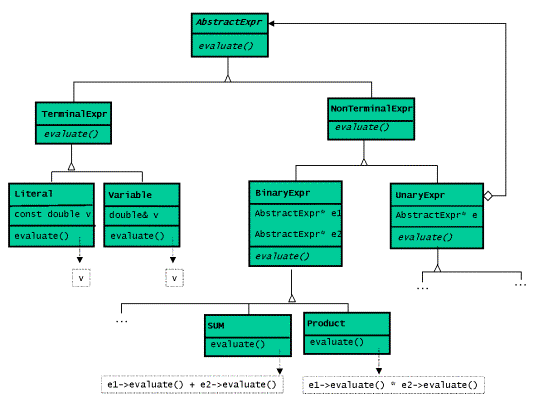
Figure 8: Class Diagram of an Object-Oriented Implementation of
an Interpreter for Arithmetic Expressions
Samples of the corresponding source code of an implementation are shown
in Listing 9. The base class for UnaryExpr is implemented in analogy
to class BinaryExpr and all the concrete unary and binary expressions follow
the example of class Sum.
| Listing 9: Object-Oriented Implementation of the Interpreter for Arithmetic Expressions |
|
class AbstractExpr { public: virtual double eval() const = 0; };
class TerminalExpr : public AbstractExpr {
class NonTerminalExpr : public AbstractExpr {
class Literal : public TerminalExpr {
class Variable : public TerminalExpr {
class BinaryExpr : public NonTerminalExpr {
class Sum : public BinaryExpr {
...
|
Listing 10 shows how the interpreter would be used for the evaluation
of the expression (x+2)*3.
| Listing 10: Using the Interpreter for Arithmetic Expressions |
|
void someFunction(double x) { Product expr(new Sum(new Variable(x),new Literal(2)), new Literal(3)); cout << expr.eval() << endl; } |
First an expression object expr is created that represents the expression (x+2)*3, and then the expression object is told to evaluate itself. Naturally, this is an utterly inefficient way to calculate the result of a primitive expression such as (x+2)*3. But hold on; we will now turn the object-oriented approach into a template-based solution.
As before in the case of the dot product, we will eliminate all abstract base classes, because template solutions are based on name commonality rather than inheritance. For this reason, we need no base classes. Instead all terminal and non-terminal expressions will be represented by stand-alone classes that happen to have an evaluation function named eval().
Next we will express all the non-terminal expressions, such as Sum or Product, as classes generated from class templates UnaryExpr and BinaryExpr, both of which are parameterized on structural information. These class template will take the types of their subexpression(s) as type template arguments. In addition, we will parameterize the expression class templates on the type of the operation that they represent, that is, the actual operation (+,-,*,/,++,--,abs,exp,log) will be provided as a function object and its type is one of the template arguments of the expression class template.
The terminal expressions will be implemented as regular (non-template) classes, pretty much like they are in the object-oriented approach.
Instead of run time recursion we will again use compile time recursion: we will replace the recursive invocation of the virtual evaluation function by recursive template instantiation of the expression class templates.
Figure 9 below shows the classes in the template-based solution:
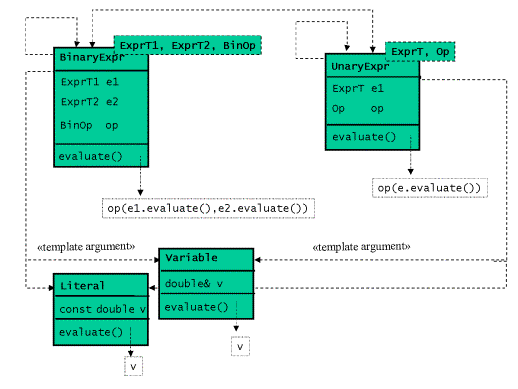
Figure 9: Class Diagram of a Template-Based Implementation of an Interpreter for Arithmetic Expressions
The source code of the implementation is shown in Listing 11.
| Listing 11: Template-Based Implementation of the Interpreter for Arithmetic Expressions |
|
class Literal { public: Literal(const double v) : _val(v) {} double eval() const { return _val; } private: const double _val; };
class Variable {
template <class ExprT1,class ExprT2, class BinOp>
...
|
The class template for UnaryExpr is implemented in analogy to class
BinaryExpr. As operations we can use the pre-defined STL function
object types plus, minus, multiplies, divides, etc. or we define our own
function object types as needed. A binary expression representing
a sum for instance would be of type BinaryExpr< ExprT1, ExprT2, plus<double>
>. Since this type name is rather unwieldy we add a creator function
for more convenient use of our solution.
| Creator Functions |
|
Creator functions are a widely used technique in
conjunction with template programming. There are many examples of
creators functions in the STL for example; make_pair() is of them. Creator
functions are convenience functions that take advantage of the fact that
the compiler automatically deduces the type arguments of function templates,
while no such automatic deduction exists for class templates.
Each time we create an object of a type that is generated from a class template, we must specify the entire generated type name including all template type arguments. Often, these generated type names are very long and hard to read and comprehend. As an example think of a pair of pairs. Its type would be something like pair< pair<string, complex<double> >, pair<string, complex<double> > >. Creator functions make life as a template user a lot easier: a creator function creates an object of a type that is generated from a class template without requiring that we type in very long type names. More precisely, creator functions are function templates and they have the same template type arguments as the class template that describes the type of the object that is to be created. In our example of pairs, the pair class template has two type arguments T1 and T2 representing the types of the contained elements, and the make_pair() creator function has the same two type arguments.
template <class T1, class T2>
A creator function is similar to a constructor: the arguments that we pass to a creator function are exactly the arguments that we would otherwise pass to the constructor of the object that is to be created. Since the compiler automatically deduces the template arguments of function templates, we need not specify all the template arguments when we call a creator function; the compiler will automatically deduce them from the arguments passed to the creator function. Instead of creating a pair via its constructor as
pair< pair<string,complex<double>>, pair<string,complex<double>
> >
we can create the pair by means of the creator function as
make_pair(make_pair(“origin”, complex<double>(0,0)),
|
We will use the creator function technique to ease creation of our expression
objects. Listing 12 below shows two examples of these creator functions:
| Listing 12: Creator Functions for Expression Objects |
|
template <class ExprT1,class ExprT2> BinaryExpr<ExprT1,ExprT2,plus<double> > makeSum(ExprT1 e1, ExprT2 e2) { return BinaryExpr<ExprT1,ExprT2,plus<double> >(e1,e2); }
template <class ExprT1,class ExprT2>
|
Listing 13 shows how the template-based implementation of an interpreter
would be used for the evaluation of the expression (x+2)*3.
| Listing 13: Using the Template-Based Interpreter for Arithmetic Expressions |
|
void someFunction (double x) { BinaryExpr< BinaryExpr < Variable,Literal,plus<double> >, Literal, multiplies<double> > expr = makeProd (makeSum (Variable(x), Literal(2)), Literal(3)); cout << expr.eval() << endl; } |
First, an expression object expr is created that represents the expression (x+2)*3, and then the expression object is told to evaluate itself. Note, that in this solution the type of the expression object already reflects the structure of the syntax tree.
Often the rather long name of the type of the expression object need not even be specified. In the example above we do not need the variable expr and could directly use the result of the creator function makeProd() for evaluation of the expression, as shown below:
cout
<< makeProd(makeSum(Variable(x),Literal(2)),Literal(3)).eval()
<< endl;
Evaluation
What have we gained by reimplementing the Interpreter pattern using templates instead of inheritance? Well, under the assumption that the compiler inlines all the creator functions and constructors and eval() functions (which is likely since all of them are trivial) the expressionmakeProd(makeSum(Variable(x),Literal(2)),Literal(3)).eval()
evaluates to nothing more than (x+2)*3.
Compare this to the effect of
Product expr(new Sum(new Variable(x),new Literal(2)), new Literal(3)).eval()
(see Listing 10). It results in a number of allocations from the heap
and subsequent constructions plus a number of invocations of the virtual
eval() function. Most likely none of the calls to eval() will be inlined
because compilers typically do not inline functions that are invoked through
a pointer.
In essence, the template-based solution is much faster at runtime than
the object-oriented implementation.
Further Elaboration of the Expression Template Solution
Let us now tweak the expression templates a bit and we will see that we turn them into something really useful. The first intended improvement addresses readability of the expression templates. We want to make an expression such asmakeProd(makeSum(Variable(x),Literal(2)),Literal(3)).eval()
more readable in the sense that it looks more or less like the expression that is represents, namely (x+2)*3 in this case. This can be achieved by means of operator overloading. We will make it look like eval((v+2)*3.0) with just a few minor modifications.
The first change is to rename the creator functions so that they are
overloaded operator; that is, we rename makeSum() into operator+(), makeProd()
into operator*(), and so on and so forth. The effect is that the
term
makeProd(makeSum(Variable(x),Literal(2)),Literal(3))
turns into
((Variable(x) + Literal(2)) * Literal(3))
That's good, but not good enough. We would like to write it as ((x+2)*3). Hence, our goal is to eliminate the creation of a Variable and a Literal, which still clutter the expression.
In order to find out how we can improve the solution let us examine
what an expression such as x+2 means, now that we renamed the creator function
makeSum() into operator+(). The implementation of operator+() is
shown in Listing 14 below.
| Listing 14: Creator Function for Sum Expression as Overloaded Operator+ |
|
template <class ExprT1,class ExprT2> BinaryExpr<ExprT1,ExprT2,plus<double> > operator+(ExprT1 e1, ExprT2 e2) { return BinaryExpr<ExprT1,ExprT2,plus<double> >(e1,e2); } |
We would like for x+2 to be the same as operator+(x,2), which formerly was makeSum(x,2). For this reason x+2 is the result of creating a binary expression object that represents a sum and which was created with the double variable x and the int literal 2 as constructor arguments. More precisely, it is an unnamed object created as BinaryExpr<double,int,plus<double>>(x,2). Note that the type of the object is not quite what we want. We need an object of type BinaryExpr<Variable,Literal,plus<double>>, but the automatic template argument deduction does not know that x is a Variable and 2 is a Literal in our context. The compiler deduces type double from argument x and type int from argument 2, because the compiler examines the types of the arguments passed to the function.
It turns out that we must nudge the compiler a little bit so that it
deduces what we need. If we passed an object of type Variable instead
of the original variable x then the automatic argument deduction would
at least yield type BinaryExpr<Variable,int,plus<double>>, which
is a little closer to the goal. (We will address the remaining int-to-Literal
conversion in a minute). For this reason, a minimal degree of cooperation
from the users' side is inevitable: they must wrap their variables into
objects of type Variable to make it work, as shown in Listing 15 below:
| Listing 15: Using the Template-Based Interpreter for Arithmetic Expressions |
|
void someFunction (double x) { Variable v = x; cout << ((v + 2) * 3).eval() << endl; } |
With the use of a Variable object v instead of a plain numeric variable we achieved that an expression such as v+2 evaluates to an unnamed object equivalent to BinaryExpr<Variable,int,plus<double>>(v,2). Such a BinaryExpr object has two data members, which are of type Variable and int respectively. The evaluation function BinaryExpr<Variable,int,plus<double>>::eval() would return the sum of the result of the evaluation of its two data members. The crux is that the int data member does not know how to evaluate itself; we need to turn the literal 2 into an object of type Literal, which does know how to evaluate itself. How can we automatically convert constants of any numerical type to objects of type Literal? In order to solve the problem we'll define expression traits.
| Traits |
|
Use of traits is another common programming technique
in conjunction with template programming. A traits class is a shadow
class that accompanies another type and contains information that is associated
with the other type.
The standard C++ library has several examples of traits: the character traits are an example. As you might know the standard string class is a class templates that is parameterized on the character type in order to allow for representation of tiny character and wide character string, at least. In principle, the string class template, which is actually named basic_string, can be instantiated on any character type, not just the two character type that are predefined by the C++ language. If for instance someone needs to represent, say Japanese, characters as a structure named Jchar, then the basic_string template can be used to create a string class for Japanese characters, namely basic_string<Jchar>. Imagine you are implementing such a string class template? You would find that there is information that you would need, but that is not contained in the character type. For instance, how would you calculate the string length? By counting all characters in the string until you find the end-of-string character. How would you know which is the end-of-string character? Okay, we know it is '\0' in the case of tiny characters of type char, and there is a corresponding end-of-string character defined for characters of type wchar_t, but how would you identify the end-of-string character for Japanese characters of type Jchar? Quite obviously the information about the end-of-string character is a piece of information that is associated with each character type, but is not contained in the character type. And this is exactly what traits are for: they provide information that is associated with a type, but is not contained in the type. A traits type is a shadow type, typically a class template that can be instantiated or specialized for a group of types and provides information associated with each type. The character traits for instance, see the char_traits class template in the standard C++ library, contains a static character constant that designates the end-of-string character for the character type it is instantiated for. |
We will apply the traits technique to solve our problem with the conversion
of numeric literals to objects of type Literal. We will define expression
traits that provide for every expression type the information about how
they should be stored inside the expression objects that they are operands
of. All entities of numeric types shall be stored as objects of type
Literal; all objects of type Variable shall be stored as they are, namely
as Variables; and all non-terminal expression objects shall also be stored
as they are. Listing 16 shows the definition of the expression traits:
| Listing 16: Expression Traits |
|
template <class ExprT> struct exprTraits { typedef ExprT expr_type; };
template <> struct exprTraits<double>
template <> struct exprTraits<int>
...
|
The expression traits class defines a nested type expr_type, which represents the expression type of an expression object. There is a general expression traits template that defines the expression type for all expressions that are class types, such as BinaryExpr, UnaryExpr or Variable. In addition there are specializations of the general class template for all those type that are built-in numeric types such as short, int, long, float, double, etc. For all non-class expressions the expression type is defined as type Literal.
Inside the definition of the BinaryExpr and UnaryExpr classes we will
use the expression traits to determine the type of the data member that
will hold the subexpression.
| Listing 17: Using the Expression Traits |
|
template <class ExprT1,class ExprT2, class BinOp> class BinaryExpr { public: BinaryExpr(ExprT1 e1, ExprT2 e2,BinOp op=BinOp()) : _expr1(e1),_expr2(e2),_op(op) {} double eval() const { return _op(_expr1.eval(),_expr2.eval()); } private: exprTraits<ExprT1>::expr_type _expr1; exprTraits<ExprT2>::expr_type _expr2; BinOp _op; }; |
Thanks to the use of the expression traits an expression object of type BinaryExpr<Variable,int,plus<double>> will contain its two operands as objects of type Variable and Literal, as desired.
Now we have achieved that an expression such as ((v + 2) * 3).eval(),
where v is a Variable that wraps a double variable x, will evaluate to
(x+2)*3. Let us do some minor tweaking to make it even more readable.
Most people find it weird to invoke a member function of something that
looks like an expression. If we define a helper function we can turn
the expression ((v + 2) * 3).eval() into something like eval((v + 2) *
3), which looks more natural to most people, but is otherwise equivalent.
Listing 18 shows the helper function:
| Listing 18: The eval() Helper Function |
|
template <class ExprT> double eval(ExprT e) { return e.eval(); } |
Figures 10 illustrates how the expression ((v + 2) * 3).eval(), where v is a Variable that wraps a double variable x, gradually unfolds at compile-time to the expression (x+2)*3.
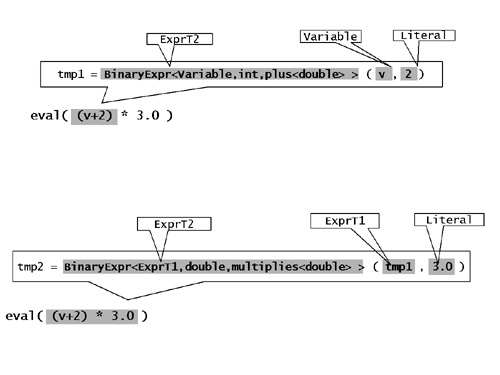
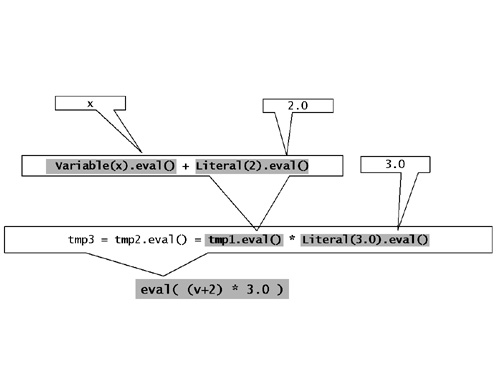
Figure 10: Compile-Time Evaluation of the Expression Object (v+2)*3
Repeated Evaluation of an Expression Object
You might still wonder where the benefit of expression objects is. Each expression object represents the syntactical decomposition of an arithmetic expression; it's a syntax tree that knows how to interpret itself to produce a numeric value. Basically, we've set up a machinery for evaluation of expressions - something that is built into the language anyway. So, what's the point? Well, a minimal further adjustment of the solution will get us to the point.So far, the interpretation of the syntax tree is rather static. Each syntax tree is created and interpreted only once. A more dynamic usage model is possible, where a given syntax tree can be evaluated repeatedly for different input values. Remember, that we ultimately want to calculate integrals such as
using an integration function such as the one below, which approximates the integral by evaluating an expression for a specifed number of equidistant points in an interval: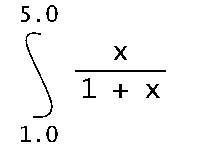
template <class ExprT>
double integrate (ExprT e,double from,double to,size_t n)
{ double sum=0, step=(to-from)/n;
for (double i=from+step/2; i<to; i+=step)
sum+=e.eval(i);
return step*sum;
}
This function could be used as shown below to approximate the integral of x/(1+x) from the example above:
Identity<double> x;
cout << integrate (x/(1.0+x),1.0,5.0,10) << endl;
Here we need an expression object that can be interpreted repeatedly,
something that our expression templates do not allow yet. It just
takes a minor modification to turn our static syntax tree interpretation
into a repeatable interpretation. We just have to change all evaluation
functions of all our expression class templates so that they accept an
input argument, namely the value for which they evaluate themselves.
The non-terminal expressions will pass on the argument on to their subexpressions.
The Literal will accept the argument and ignore it; it will continue returning
the constant value that it represents. The Variable will no longer
return the value of a variable that it refers to, but will return the value
of its argument. For this reason we rename it to Identity.
Listing 19 below shows the modified classes:
| Listing 19: Expression Templates with Repeatable Evaluation |
|
class Literal { public: Literal(double v) : _val(v) {} double eval(double) const { return _val; } private: const double _val; };
template<class T>
template <class ExprT1,class ExprT2, class BinOp>
...
|
If we add non-terminal expressions for incorporation of numeric functions
such as sqrt(), sqr(), exp(), log(), etc. we can even calculate the Gauss
distribution:
| Listing 20: Calculating the Gauss Distribution |
|
double sigma=2.0, mean=5.0; const double Pi = 3.141593; cout << integrate( 1.0/(sqrt(2*Pi)*sigma) * exp(sqr(x-mean)/(-2*sigma*sigma)), 2.0,10.0,100) << endl; |
For providing the expressions that represent numeric functions we can
use the functions that come with the standard C library. All we need
to do is adding creator functions for unary or binary expressions whose
operation is one of the predefined C functions. Listing 21 below
shows a couple of examples:
| Listing 21: Numeric Functions as Non-Terminal Expression Templates |
|
template <class ExprT> UnaryExpr<ExprT,double(*)(double)> sqrt(const ExprT& e) {return UnaryExpr<ExprT,double(*)(double)>(e,::std::sqrt);}
template <class ExprT>
...
|
With these additions in place we now have a powerful and high-performance solution for evaluation of arithmetic expressions. It is not much of a stretch to imagine that application of the techniques demonstrated in this article allows setting up expression templates for logical expressions. By renaming the evaluation function from eval() to operator()(), which is the function call operator, we can easily turn the expression objects into function objects, which can then be used in conjunction with STL algorithms. Below is an example of a logical expression that is used as a predicate for counting elements in a list:
list<int> l;
Identity<int> x;
count_if(l.begin(),l.end(), x >= 0 && x <= 100 );
The example nicely illustrates the gain in readability that expression
templates enable, at zero cost in terms of runtime performance. Provided
that the expression templates are already in place they are easy and convenient
to use. Building an expression template library is a different story;
it involves many more template programming techniques than we've discussed
in this article. However, all template libraries are built on principles
like the ones discussed in this article.
References
Quite a number of expression template libraries are available for free download, some of which are mentioned in the list of reference below. However, the list by no means claims to be comprehensive or representative. If you are interested in further information we recommend commencing your search at one of the directories (see / JÜL / and / OON /).| /GOF/ |
Design Patterns: Elements of Reusable Object-Oriented Software
Erich Gamma, Richard Helm, Ralph Johnson, John Vlissides Addison-Wesley, January 1995 ISBN: 0201633612 |
| /VAN/ |
C++ Templates – The Complete Guide
David Vandevoorde and Nicolai Josuttis Addison-Wesley 2003 |
| /UNR/ |
Compile-Time Computation of Prime Numbers
Erwin Unruh http://www.erwin-unruh.de/Prim.html |
| /DUR/ |
Design Patterns for Generic Programming in C++
Alexandre Duret-Lutz, Thierry Géraud, and Akim Demaille http://www.lrde.epita.fr/dload/papers/coots01.html |
| /VEL/ |
T. Veldhuizen, "Expression Templates," C++ Report, Vol. 7 No. 5 June
1995, pp. 26-31
The article has been reprinted in the book "C++ Gems" edited by Stanley Lippman. http://osl.iu.edu/~tveldhui/papers/Expression-Templates/exprtmpl.html |
| /JÜL/ |
Research Centre Jülich
http://www.fz-juelich.de/zam/cxx/ An impressive directory of C++ resources such as books, articles, FAQs, other C++ pages, compilers, libraries, etc. See in particular the links to other C++ libraries at http://www.fz-juelich.de/zam/cxx/extmain.html#lib |
| /OON/ |
The Object-Oriented Numerics Page
http://www.oonumerics.org/oon/#libraries A directory of links to freely available numeric libraries. |
| /BLI/ |
The Blitz Project
http://oonumerics.org/blitz/ A C++ class library for scientific computing which uses template techniques to achieve high performance. |
| /PET/ |
PETE (Portable Expression Template Engine)
http://acts.nersc.gov/events/PI1999/pete/ A portable C++ framework to easily add powerful expression templates. |
| /POO/ |
POOMA (Parallel Object-Oriented Methods and Applications)
http://acts.nersc.gov/pooma/ An object-oriented framework for applications in computational science requiring high-performance parallel computers. |
| /MET/ |
MET (Matrix Expression Templates)
http://met.sourceforge.net/ A C++ matrix class library. C++ overloaded operators enable one to write the simplest code like u = m*v + w. |
| /MTL/ |
MTL (Matrix Template Library)
http://www.osl.iu.edu/research/mtl/ A high-performance generic component library that provides linear algebra functionality for a wide variety of matrix formats. Uses an STL-style approach. Provides generic algorithms corresponding to the mathematical operations that define linear algebra. Containers, adaptors, and iterators are used to represent and to manipulate matrices and vectors. See also the following paper: The Matrix Template Library: A Generic Programming Approach to High-Performance Jeremy G. Siek and Andrew Lumsdaine http://www.osl.iu.edu/download/research/mtl/papers/iscope_final.pdf |
| /FAC/ |
FACT! (Functional Additions to C++ through Templates and Classes)
http://www.kfa-juelich.de/zam/FACT/start/index.html A library that offers lambda expressions built on top of PETE . By using FACT!'s lambda syntax the programmer can define generic functions for use with the STL on the fly. |
| /FCP/ |
FC++ (Functional Programming in C++)
http://www.cc.gatech.edu/~yannis/fc++/ A library for functional programming in C++, which you can use to define your own higher-order polymorphic functions. |
| /BLL/ |
BLL (The Boost Lambda Library)
http://www.boost.org/libs/lambda/doc/index.html A C++ template library, which implements lambda abstractions for C++. The primary motivation for the BLL is to provide flexible and convenient means to define unnamed function objects for STL algorithms. |
| /PHO/ |
Phoenix (A parser used by
Spirit
)
http://spirit.sourceforge.net/index.php?doc=docs/phoenix_v1_0/index.html Phoenix is a framework that opens up functional programming techniques such as Lambda (unnamed functions) and Currying (partial function evaluation), similar to FC++ and BLL. |
Acknowledgements
Our thanks to Gary Powell, who read our article in CUJ and sent us email. He brought FACT!, FC++, the Boost Lambda Library, and Phoenix to our attention.|
If you are interested to hear more about this and related topics you might want to check out the following seminar: |
||
Seminar
|
||